Coding a simple (random) Multi-Armed Bandit Agent
Coding a simple (random) Multi-Armed Bandit Agent#
In this section, we shall code a simple MAB agent. The idea here is to create the example of slot machines explained in the previous page to understand the working of a simple MAB agent.
We shall have some slot machines each with a distribution of reward. User shall pick a slot machine independently at a time to receive a reward. Each selection is independent to its previous selection as the current setting does not make any decision using previous data.
Feel free to explore the slot machines by using the live code option on the top of this page.
Bandits with Gaussian Reward distribution
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Class for a single slot machine. Rewards are Gaussian.
class GaussianBandit(object):
def __init__(self, mean=0, stdev=1):
self.mean = mean
self.stdev = stdev
def pull_lever(self):
reward = np.random.normal(self.mean, self.stdev)
return np.round(reward, 1)
# Class to initialize all Gaussian bandits and play the game.
class GaussianBanditGame(object):
def __init__(self, bandits):
self.bandits = bandits
# np.random.shuffle(self.bandits)
self.reset_game()
def play(self, choice):
reward = self.bandits[choice - 1].pull_lever()
self.rewards.append(reward)
self.total_reward += reward
self.n_played += 1
return reward
def user_play(self):
self.reset_game()
print("Game started. " +
"Enter 0 as input to end the game.")
while True:
print(f"\n -- Round {self.n_played}")
choice = int(input(f"Choose a machine " +
f"from 1 to {len(self.bandits)}: "))
if choice in range(1, len(self.bandits) + 1):
reward = self.play(choice)
print(f"Machine {choice} gave " +
f"a reward of {reward}.")
avg_rew = self.total_reward/self.n_played
print(f"Your average reward " +
f"so far is {avg_rew}.")
else:
break
print("Game has ended.")
if self.n_played > 0:
print(f"Total reward is {self.total_reward}" +
f" after {self.n_played} round(s).")
avg_rew = self.total_reward/self.n_played
print(f"Average reward is {avg_rew}.")
def user_play_random_pick(self):
avg_reward = []
self.reset_game()
print("Game started.")
for i in range(10000):
choice = np.random.choice(3)+1
reward = self.play(choice)
avg_rew = self.total_reward/self.n_played
avg_reward.append(avg_rew)
print("Game has ended.")
if self.n_played > 0:
print(f"Total reward is {self.total_reward}" +
f" after {self.n_played} round(s).")
avg_rew = self.total_reward/self.n_played
print(f"Average reward is {avg_rew}.")
plt.plot(avg_reward)
plt.title("Average Rewards")
plt.show()
def user_play_exploit_pick(self):
avg_reward = []
self.reset_game()
print("Game started.")
for i in range(10000):
choice = 2
reward = self.play(choice)
avg_rew = self.total_reward/self.n_played
avg_reward.append(avg_rew)
print("Game has ended.")
if self.n_played > 0:
print(f"Total reward is {self.total_reward}" +
f" after {self.n_played} round(s).")
avg_rew = self.total_reward/self.n_played
print(f"Average reward is {avg_rew}.")
plt.plot(avg_reward)
plt.title("Average Rewards")
plt.show()
def reset_game(self):
self.rewards = []
self.total_reward = 0
self.n_played = 0
slotA = GaussianBandit(5, 3)
slotB = GaussianBandit(6, 2) # Best slot machine with highest reward
slotC = GaussianBandit(1, 5)
game = GaussianBanditGame([slotA, slotB, slotC])
#game.user_play()
# Automating the slot picking using random decision and visualizing the reward
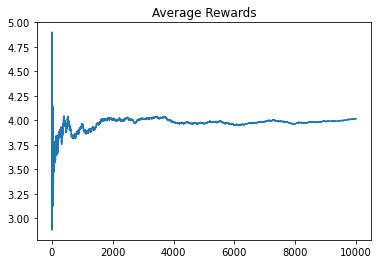
game.user_play_random_pick()
Game started.
Game has ended.
Total reward is 40178.00000000014 after 10000 round(s).
Average reward is 4.017800000000014.
# Reward if the agent always picks the best slot machine
game.user_play_exploit_pick()
Game started.
Game has ended.
Total reward is 59965.70000000002 after 10000 round(s).
Average reward is 5.996570000000002.
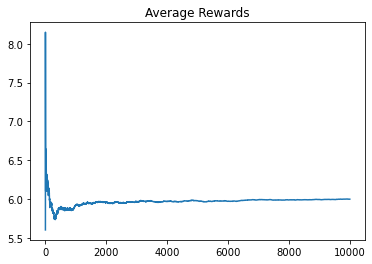
From the above results, we see that with increased number of trails, the average reward per individual slot machine converges the true mean. This is perfectly in lines with Law of Large numbers. This can be seen when the agent always picks the best slot machine. The estimated mean converges to 6.018.
Slot machines with a fixed probability of binary reward.
## Multi-Arm Bandit code
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
Bandit_probs= [0.9,0.8,0.5]
num_trails = 10000
class Bandit:
def __init__(self, prob):
self.actual_prob = prob
self.prob_estimate = 0
self.N = 0
def pull(self):
return np.random.random()<self.actual_prob
def update(self,x):
self.N+=1
self.prob_estimate+=(1/self.N)*(x-self.prob_estimate)
return self.prob_estimate
def experiment():
bandits = [Bandit(p) for p in Bandit_probs]
rewards = np.zeros(num_trails)
slot_rew = [[], [], []]
num_steps = 0
num_optimal = 0
optimal_j = np.argmax([b.actual_prob for b in bandits])
for i in range(num_trails):
j = np.random.choice(len(bandits))
num_steps +=1
if j == optimal_j:
num_optimal+=1
rewards[i] = bandits[j].pull()
curr_estimate = bandits[j].update(rewards[i])
slot_rew[j].append(curr_estimate)
for b in bandits:
print("Estimated probabilities", b.prob_estimate)
print("Total reward earned = ", rewards.sum())
print("Overall win rate = ", rewards.sum()/num_trails)
print("Number of optimal pulls = ", num_optimal)
for i in range(len(slot_rew)):
plt.plot(slot_rew[i], label = "Slot machine with reward probability {}".format(Bandit_probs[i]))
plt.plot(np.ones(len(slot_rew[i]))*(Bandit_probs[i]), label = 'actual probability {}'.format(Bandit_probs[i]))
plt.legend()
plt.title("Agent choosing random independent action")
plt.show()
if __name__ == "__main__":
experiment()
Estimated probabilities 0.9031668696711337
Estimated probabilities 0.8046224961479185
Estimated probabilities 0.493229616825122
Total reward earned = 7289.0
Overall win rate = 0.7289
Number of optimal pulls = 3284
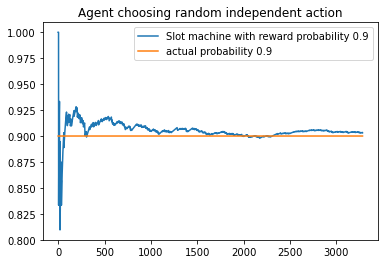
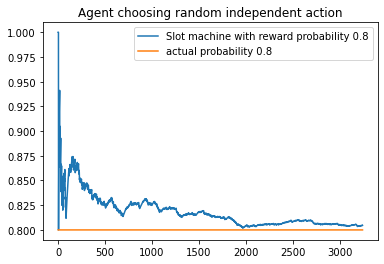
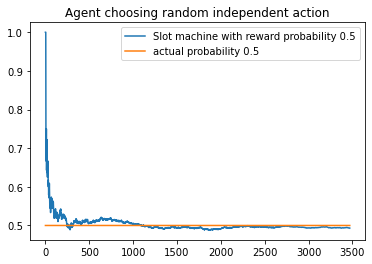
In the above example code, the agent receives a reward of 1 or 0 based on the probability of reward of individual bandits. It is clearly seen that even with an agent with completely random actions, the estimated probabilities for reward and the true probabilities for reward converge at around 1500 time steps.
Consider pondering if 1500 time steps are sufficient or considerable to stop exploring. Is there a better way where we do not lose upon the reward by choosing suboptimal bandits? We shall explore those solutions in the next page.
To understand the code better try making changes to the reward function, the update function and try creating some plots too. Trust me you cant break the existing code.
